두 개 이상의 다수 집단 간 평균은 비교하는 분산분석에서 일원배치 분산분석을 복습해 보자.
이 전엔 독립표본 T-검정에 대해서 정리하면서 복습해 보았다.
독립표본 T-검정
두 집간 간의 평균 차이를 검정하는 T검정에서 독립표본 T-검정을 복습해보자. 기본가정 정규성 만족 (아닐 시 윌콕슨이 부호 순위 검정, 맨휘트니 검정) 등분산성 만족 (아닐 시 Welch`s t-test) 종속
py-moon.tistory.com
기본가정 및 조건
- 정규성, 독립성을 만족한다 (아닐 시 Kruskal-Wallis test진행)
- 등분산성을 만족한다 (아닐 시 Welch`s ANOVA진행)
- 종속변수는 1개 연속형, 독립변수는 1개 범주형
- 사후검정 진행
- 주효과(각각의 요인에 의한 효과)
일원배치 분산분석은 iris데이터를 활용해서 정리하고자 한다.
|
1
2
3
4
5
6
7
8
|
import pandas as pd
import scipy.stats as stats
import seaborn as sns
import matplotlib.pyplot as plt
Iris_data = pd.read_csv('data/iris.csv')
Iris_data.head(5)
|
cs |
> 분석에 필요한 코드와 데이터를 불러온다.
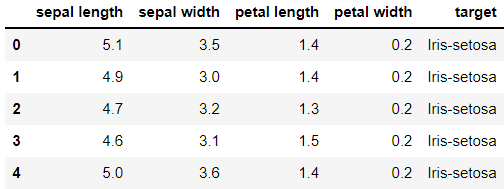
> head를 사용해서 상위 5개의 데이터를 확인하고 변수들을 확인한다.
|
1
2
3
4
5
6
|
Iris_data.target.value_counts()
Iris-setosa 50
Iris-versicolor 50
Iris-virginica 50
|
cs |
> target 변수의 고윳값 개수를 각각 확인해 보니, 3개의 고윳값이 있고 각각 50개씩 고르게 분포되어 있었다.
|
1
2
3
4
5
|
target_list = Iris_data['target'].unique()
setosa = Iris_data[Iris_data['target']==target_list[0]]['sepal width']
versicolor = Iris_data[Iris_data['target']==target_list[1]]['sepal width']
virginica = Iris_data[Iris_data['target']==target_list[2]]['sepal width']
|
cs |
> target 변수의 고윳값들을 list형태로 target_list 변수에 할당해 주었다.
> 그리고, 각각의 종류에 대해서 sepal width(꽃받침의 너비) 변수를 각각 할당해 주었다.
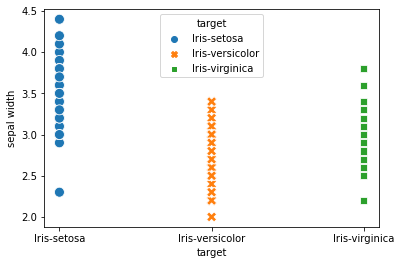
> 중간과정을 시각화해보았다.
> 각각의 꽃의 종류별로 꽃받침의 너비의 분포를 알 수 있다.
> 종류별로 꽃받침 너비의 차이가 있어 보인다. 이 차이가 통계적으로 유의한 차인지 확인해보고자 한다.
> 우선, 정규성 검정을 실시한다.
|
1
2
3
|
print("setosa 변수의 정규성 결과", stats.shapiro(setosa))
print("versicolor 변수의 정규성 결과", stats.shapiro(versicolor))
print("virginica 변수의 정규성 결과", stats.shapiro(virginica))
|
cs |
> 샤피로 윌크 검정으로 세 변수에 대해서 정규성 검정을 실시하였다.
귀무가설 : 해당 변수는 정규성을 만족한다.
대립가설 : 해당 변수는 정규성을 만족하지 않는다.
|
1
2
3
|
setosa 변수의 정규성 결과 ShapiroResult(statistic=0.968691885471344, pvalue=0.20465604960918427)
versicolor 변수의 정규성 결과 ShapiroResult(statistic=0.9741330742835999, pvalue=0.33798879384994507)
virginica 변수의 정규성 결과 ShapiroResult(statistic=0.9673910140991211, pvalue=0.1809043288230896)
|
cs |
> 세 결과 모두 유의확률(pvalue)이 유의 수준(0.05) 보다 크으므로 귀무가설을 채택한다.
> 즉, 세 집단은 모두 정규분포를 이루고 있다.
> 다음으로 등분산성 검정을 실시한다.
|
1
|
print("등분산성 검정 결과 :", stats.levene(setosa, versicolor, virginica))
|
cs |
> 세 변수에 대해서 등분산 검정을 위해 Levene검정을 실시해 봤다.
귀무가설 : 세 집단의 분산이 등분산을 이룬다.
대립가설 : 세 집단의 분산이 서로 다른 이분산을 이룬다.
|
1
|
등분산성 검정 결과 : LeveneResult(statistic=0.6475222363405327, pvalue=0.5248269975064537)
|
cs |
> 실시한 결과에서 유의확률(pvalue)이 유의 수준(0.05) 보다 크으므로 귀무가설을 채택한다.
> 즉, 세 집단은 서로 분산이 같은 등분산을 이룬다.
> 두 조건(정규성, 등분산성)을 만족했으니 일원배치 분산분석을 실시한다.
|
1
|
print("일원배치 ANOVA 검정 결과 :", stats.f_oneway(setosa, versicolor, virginica))
|
cs |
> stats.f_oneway를 사용해서 세 집단의 평균이 유의한 차이를 가지는지 알아보자.
귀무가설 : 세 집단에 대해서 sepal width(꽃받침 너비)의 평균은 같다,
대립가설 : 세 집단에 대해서 sepal width(꽃받침 너비)의 평균은 유의한 차이를 가진다.
|
1
|
일원배치 ANOVA 검정 결과 : F_onewayResult(statistic=47.36446140299382, pvalue=1.3279165184572242e-16)
|
cs |
> 알아본 결과에서 유의확률(pvalue)이 유의수준(0.05)보다 작으므로 귀무가설을 기각하고 대립가설을 채택한다.
> 즉, 세 집단의 꽃받침 너비의 평균은 서로 유의한 차이를 가진다.
> 그렇다면, 특히 어떤 종류들 간에 꽃받침의 너비에 차이가 있는지 사후검정을 통해 알아보자.
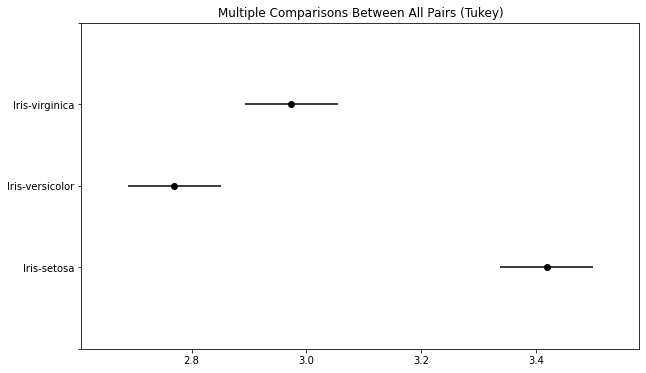
귀무가설 : 세 집단들 사이의 평균은 같다.
대립가설 : 세 집단들 사이의 평균은 유의미한 차이가 있다.
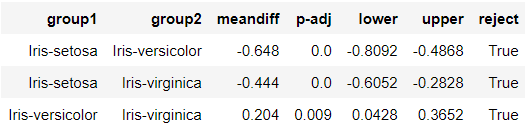
> 결과를 살펴보면, p-adj(수정된 pvalue)가 모두 유의수준(0.05)보다 작으므로 모두 귀무가설을 기각하고 대립가설을 채택한다.
> 즉, 세 집단들 사이의 평균은 유의미한 차이가 있다는 결론이다.
OUTTRO.
나에게 통계분석은 언제, 어느 순간에 해야 하는 것인가를 헷갈리게 하는 존재다.
하지만 하나하나 뜯어가며 정리를 해보니 앞에 정리했었던 T검정과 분산분석의 차이점을 알 수 있었다.
확실히 정리하기 전후로 이해하는 정도의 차이는 분명하다.
앞으로 해야 할 분석과제들이 수없이 쌓여있는데 가설검정과 좀 더 친해져야겠다.
'내가 하는 데이터분석 > 내가 하는 통계분석' 카테고리의 다른 글
| [선형 회귀분석, Linear Regression] with Python (0) | 2023.01.08 |
|---|---|
| [이원배치 분산분석, Two-way ANOVA] with Python (0) | 2023.01.06 |
| [독립표본 T-검정, Independent Sample T-Test] with Python (0) | 2022.12.29 |
| [대응표본 T-검정, Paired Samles T-Test] with Python (2) | 2022.12.27 |
| [일표본 T-검정, One Sample T-Test] with Python (0) | 2022.12.25 |



