머신러닝 기법 중 단순 선형 회귀모델에 대해 다뤄보며 정리하고자 한다.
선형 회귀는 입력(하나의 독립변수)에 대한 선형함수를 만들어 미래를 예측하는 알고리즘이다.
예를 들어, 나이에 따른 의료비 지출에 대한 선형 회귀 모델을 만들어본다면, 나이가 독립변수가 되고 의료비가 종속변수가 된다.
여기서 선형 모델의 파라미터인 가중치 합과 편향을 가지고 예측을 수행한다.
회귀모델에서 많이 사용하는 성능평가지표는 MSE(Mean Square Error:평균 제곱 오차)이다.
이를 최소화하는 모델이 흔히 말하는 좋은 모델이라 말할 수 있다.
이전의 통계분석에서도 선형 회귀를 다룬 적이 있지만,
선형 회귀분석(Linear Regression) with Python
하나 혹은 그 이상의 원인(독립변수)이 종속변수에 미치는 영향을 추적해서 식으로 표현하는 회귀분석을 복습해 보자. 이 전엔 이원배치 분산분석(Two-way ANOVA)에 대해서 정리해 보았다. 이원배치
py-moon.tistory.com
이번에는 모델과 경사하강법을 사용하여 문제를 해결하고자 한다.
|
1
2
3
4
5
6
7
|
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
data = pd.read_csv('data/insurance.csv')
|
cs |
> 선형 회귀 모델을 구현하기 위해 캐글의 insurance데이터를 활용한다.
> 모델 구현을 위한 라이브러리와 데이터를 불러와준다.
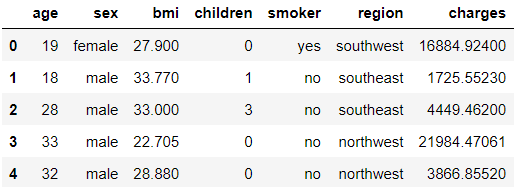
> head()를 통해서 데이터를 대략적으로 확인해 본다.
|
1
2
3
4
5
6
7
|
x = data['age']
y = data['charges']
plt.figure(figsize = (10, 5))
plt.scatter(x, y)
plt.xlabel('Age')
plt.ylabel('Charges')
|
cs |
> 독립변수인 age변수를 x로, 종속변수인 charges변수를 y로 할당해 준다.
> 모델을 구축하기 전 산점도를 통해서 독립변수와 종속변수 간에 존재하는 선형성을 우선 확인해 본다.
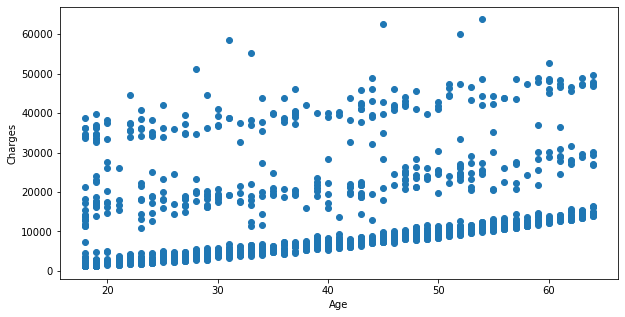
> 그 결과, 선형성이 존재하는 것을 확인할 수 있다.
|
1
2
3
4
5
6
|
x = np.array(data['age'])
y = np.array(data['charges'])
x = x.reshape(1338, 1)
y = y.reshape(1338, 1)
lr = LinearRegression()
lr.fit(x, y)
|
cs |
> 선형회귀 객체를 생성해서 fit()을 통해 학습을 시키기면 사실상 모델구축은 끝이다.
> 하지만, 입력되는 두 변수 모두 2차원 배열이 되어야 하므로 reshape()를 통해서 차원을 맞춰준다.
|
1
2
3
4
5
6
|
print('절편 :', lr.intercept_, '계수 :', lr.coef_)
print('결정계수 :', lr.score(x, y))
절편 : [3165.88500606] 계수 : [[257.72261867]]
결정계수 : 0.08940589967885804
|
cs |
> 중간과정 없이 단순하게 학습된 모델의 절편과 계수를 확인하고, 이 모델이 데이터를 얼마나 설명하는지 나타내는 결정계수까지 확인해 본다.
> 결과, 결정계수를 확인해 보면 약 8%를 설명한다고 볼 수 있다. 좋은 결과는 아닌 것 같다.
|
1
2
3
4
5
6
7
8
9
|
x_new = [[19], [64]]
y_hat = lr.predict(x_new)
print('19세의 예상 의료비용 :', y_hat[0])
print('64세의 예상 의료비용 :', y_hat[1])
19세의 예상 의료비용 : [8062.61476073]
64세의 예상 의료비용 : [19660.13260074]
|
cs |
> 예측된 값들을 예시로 확인해 보기 위해 19세와 64세의 예상 의료비용을 찍어보았다.
> 그 결과 19세의 예상 의료비용은 약 8,062달러이고 64세의 예상 의료비용은 약 19,660달러로 확인되었다.
|
1
2
3
4
5
|
plt.figure(figsize = (10, 5))
plt.plot(x_new, y_hat, '-r')
plt.plot(x, y, 'b.')
plt.xlabel('Age')
plt.ylabel('Charges')
|
cs |
> 원본 데이터와 예측 회귀선 사이의 형태를 알아보기 위해 시각화해보았다.
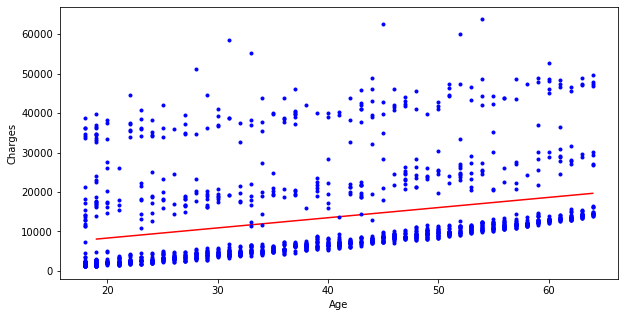
> 파란 점은 원본 데이터이고, 빨간 선은 예측된 회귀선이다.
> 산점도 그래프를 통해서 확인할 수 있듯이 예측된 데이터의 분포가 낮은 의료비용에 많이 분포되어 있다.
> 그래서인지 적색 라인이 전체적으로 낮음을 알 수 있다.
이번엔 확률적 경사하강법(SGDRegressor)을 이용한 회귀모델을 구축하고자 한다.
경사하강법은 에러가 낮아지는 방향으로 독립변수의 값은 바꿔가면서 최종적으로 가장 낮은 에러값을 갖는 독립변숫값을 찾는 방법이다.
이러한 원리를 이용해서 회귀모델을 구축해 보자.
|
1
2
3
4
5
6
7
8
9
|
from sklearn.linear_model import SGDRegressor
x = np.array(data['age'])
y = np.array(data['charges'])
x = x.reshape(1338, 1)
y = y.reshape(1338, 1)
sgd = SGDRegressor(max_iter = 1000, random_state = 2023)
sgd.fit(x, y.ravel())
|
cs |
> 위에서와 마찬가지로 차원을 맞춰준 후에 모델을 학습시킨다.
|
1
2
3
4
|
print('절편 :', sgd.intercept_, '계수 :', sgd.coef_)
절편 : [-2189.33806509] 계수 : [387.38252888]
|
cs |
> 단순 선형 회귀모델에서와 바뀐 절편과 계수를 확인한다.
|
1
2
3
4
5
6
7
8
9
|
x_new = [[19], [64]]
y_hat = sgd.predict(x_new)
print('19세의 예상 의료비용 :', y_hat[0])
print('64세의 예상 의료비용 :', y_hat[1])
19세의 예상 의료비용 : 5170.929983596192
64세의 예상 의료비용 : 22603.14378311037
|
cs |
> 당연히 그에 따라 바뀐 예측치도 확인해 준다.
> 19세의 예상 의료비용은 약 5,170달러이고 64세의 예상 의료비용은 약 22,603달러로 확인된다.
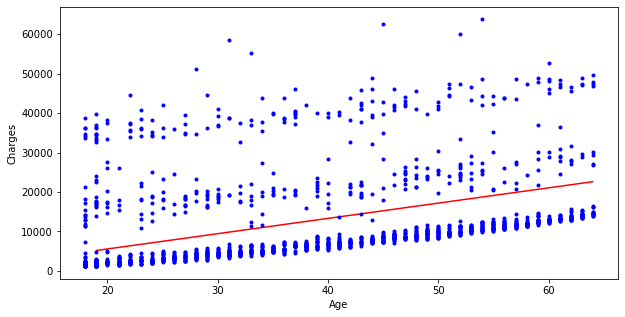
> 원본 데이터와 확률적 경사하강법으로 학습시킨 모델의 예측 회귀선을 확인해 본다.
> 단순 선형 회귀모델과 차이점은 회귀선의 경사가 좀 더 급해짐으로 인해 직관적인 견해로는 fitting이 더 잘된듯한 모습이다.
OUTTRO.
단순 선형 회귀모델과 경사하강법 원리를 이용한 SGDRegressor를 활용해서 각각의 모델들을 구축해 보았다.
각 모델마다 회귀식에 대한 결과도 산점도를 통해서 나타내보았다.
공통점은 하나의 독립변수, 하나의 종속변수를 가지고 최적의 방정식을 찾는 점이다.
차이점은 SGDRegressor가 더 최적화된 알고리즘을 가지고 있다는 점이다.
이 글에선 전처리나 EDA를 통해서 더 좋은 모델을 만드는 것이 목적이 아니다.
올해 있을 ADP실시를 대비함과 동시에 직접 실습해 봄으로써 분석과의 이질감을 없애는 용도로 이용하고 있고, 앞으로도 그럴 예정이다.
'내가 하는 데이터분석 > 내가 하는 머신러닝' 카테고리의 다른 글
| [K-최근접 이웃, K-Nearest Neighbor] KNN with Python (0) | 2023.02.07 |
|---|---|
| [서포트 벡터 머신, Support Vector Machine] SVM with Python (2) | 2023.02.05 |
| [로지스틱 회귀, Logistic Regression] with Python (0) | 2023.02.03 |
| [다중 회귀, Multiple Regression] with Python (0) | 2023.02.01 |
| [다항 회귀, Polynomial Regression] with Python (0) | 2023.01.30 |



