각 객체의 유사성을 측정해서 유사성이 높은 대상집단을 분류하는 군집분석을 정리해 보자.
계층적 군집분석은 저번에 정리해 보았다.
군집분석(Clustering) - 계층적 군집분석
각 객체의 유사성을 측정해서 유사성이 높은 대상집단을 분류하는 군집분석을 정리해 보자. 그중에서 군집의 수를 미리 정하지 않는 방식으로 군집을 형성하는 계층적 군집분석에 대해서 정리
py-moon.tistory.com
오늘은 군집의 수를 미리 정해놓고 군집을 형성하는 비계층적(분할적) 군집분석에 대해서 정리해 보자.
비계층적 군집분석에서는 K-means 군집분석과 혼합분포 군집분석에 대해서 다룰 예정이다.
종속변수가 존재하지 않는 군집분석은 비지도 학습이다.
K-means 비계층적 알고리즘의 단계
- 군집 수의 설정
- 각 군집의 중심점의 선정
- 각 개체의 배치
- 개체의 재배치
- 알고리즘의 종료
비계층적 군집분석 중에서 K-means 군집분석을 수행하기 위해 Iris데이터를 사용한다.
|
1
2
3
4
5
6
7
|
import pandas as pd
from sklearn.cluster import KMeans
import warnings
warnings.filterwarnings('ignore')
iris = pd.read_csv('data/iris.csv')
X = iris.drop(['target'], axis=1)
|
cs |
> 먼저 K-means 군집분석을 진행하기 위한 라이브러리와 데이터를 불러온다.
> 그리고 비지도학습이기 때문에 target변수를 제거해 준다.
> head()를 사용해서 상위 5개 데이터를 확인해 본다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
from sklearn.metrics import calinski_harabasz_score
for k in range(2, 10):
kmeans_model = KMeans(n_clusters=k, random_state=2022).fit(X)
labels = kmeans_model.labels_
print(calinski_harabasz_score(X, labels))
513.3038433517568
560.3999242466402
529.3982941434155
494.0943819140987
474.41697618270837
446.61798049117385
441.78817878788817
410.3153933237118
|
cs |
> K-meas 군집분석에서 군집의 개수를 선정하기 위해 calinski_harabasz_score()를 사용한다.
> calinski_harabasz_score는 클러스터 간 분산과 클러스터 내 분산의 합 비율 점수를 수치로 반환한다. 이 점수가 높게 나오는 군집의 개수를 정하는 것이 합리적이다.
> 위 결과를 통해서 군집의 개수가 3개일 때 점수가 약 560으로 가장 높게 나왔다.
> 따라서, 우리는 적절한 군집의 개수를 3개로 유추할 수 있다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
import matplotlib.pyplot as plt
def elbow(X):
sse=[] # 오차제곱합
for i in range(1, 11):
km=KMeans(n_clusters = i, random_state = 2022).fit(X)
sse.append(km.inertia_)
plt.plot(range(1, 11), sse, marker = 'o')
plt.xlabel('The Number of Clusters')
plt.ylabel('SSE')
plt.show()
print(sse)
elbow(X)
|
cs |
> 군집의 개수를 정하는 방법 중 엘보우 기법이라는 방법도 있다.
> 오차제곱합인 SSE가 감소하는 폭이 낮아지는 시점의 수치로 군집의 개수를 정하는 방법이다.

> 위 그래프를 보면 군집의 개수가 3개일 때 SSE의 감소폭이 완만해지는 것을 확인할 수 있다.
|
1
2
3
|
[680.8244, 152.36870647733906, 78.94084142614601,
57.31787321428571, 46.535582051282056, 38.964787851037855,
34.49095451505017, 29.88917890442891, 28.040190262953423, 26.061853041695148]
|
cs |
> 수치로 확인해 보아도 3번째 값부터 확실히 낮게 줄어드는 것을 확인할 수 있다.
> 따라서 우리는 군집의 개수를 3개로 최종적으로 선정하여 진행한다.
> 여기까지가 K-means 비계층적 알고리즘의 단계를 나타내어주고 있다.
|
1
2
3
4
5
6
|
km = KMeans(n_clusters = 3, random_state= 2022)
km.fit(X)
new_labels = km.labels_
iris['cluster'] = new_labels
iris.groupby(['cluster']).mean()
|
cs |
> 3개로 군집을 나눴을 때 나타나는 군집별 특성을 확인해 보자.

> 첫 번째(0번) 군집을 예시로 해석하자면 다른 군집보다 sepal length는 크고, sepal width는 작다. 그리고 petal length, petal width는 중간정도의 크기를 가진다고 볼 수 있다.
> 이 과정을 제대로 검증하기 위해서는 ANOVA분석을 진행해 보는 것이 좋다고 한다.
|
1
2
3
4
|
import seaborn as sns
sns.pairplot(iris, diag_kind = 'kde', hue = 'cluster', corner = True, palette = 'bright')
plt.show()
|
cs |
> 하지만 시각화로 그 과정을 대체하려 한다.

> 해당 결과를 시각화해본 결과 변수들의 특징대로 3개의 군집으로 나름 잘 구분이 딘 것을 볼 수 있다.
> 그중 1번 군집은 0번, 2번 군집에 비해 독보적으로 잘 분리가 되는 특징을 가지는 것을 확인할 수 있다.
> K-means군집분석을 calinski_harabasz_score와 엘보우 기법을 활용해서 군집의 개수를 정하고, 정한 군집의 개수로 구분을 지었을 때 만족스러운 결과가 도출되었다.
비계층적 군집분석 중에서 혼합분포 군집분석을 수행하기 위해 Iris데이터를 사용한다.
|
1
2
3
4
5
6
7
|
import pandas as pd
import numpy as np
from sklearn.preprocessing import StandardScaler
from sklearn.mixture import GaussianMixture
iris = pd.read_csv('data/iris.csv')
df = iris.drop('target', axis=1)
|
cs |
> 혼합분포 군집분석을 수행하기 위한 라이브러리와 데이터를 불러온다.
> 마찬가지로 비지도학습이기 때문에 target변수를 제거해 준다.
> 혼합분포는 모형을 기반으로 하는 군집분석이다.
> 데이터가 k개의 모수적 모형의 가중합으로 표현되는 모집단 모형으로부터 나왔다는 가정하에서 모수와 함께 가중치를 자료로부터 추정하는 방법을 사용한다고 한다.
> 혼합분포 군집분석은 확률 분포를 도입한 분석이기 때문에 K-means보다 통계적으로 엄밀한 결과를 얻을 수 있다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
scaler = StandardScaler()
df_scaled = scaler.fit_transform(df)
gmm = GaussianMixture(n_components = 3)
gmm.fit(df_scaled)
gmm_labels = gmm.predict(df_scaled)
gmm_labels
array([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 0, 2, 0, 2, 0, 2, 2, 2, 2, 0, 2, 2, 2, 2, 2, 0, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
|
cs |
> 우리는 정규화시킨 데이터를 정규분포에서 군집의 개수를 3개로 하는
|
1
2
|
df['gmm_cluster'] = gmm_labels
df.groupby('gmm_cluster').mean()
|
cs |
> 구분된 군집들의 특성을 살펴보기 위해 수치로 표현해보았다.
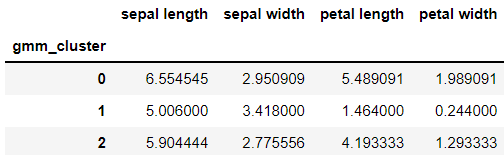
> 각각의 군집에 대해 특성을 알 수 있고, 이 수치를 활용해서 시각화하면 아래와 같다.

> 혼합분포 군집분석을 시각화한 결과를 보면 색으로 잘 구분되어 있는 모습을 확인할 수 있다.
OUTTRO.
첫 번째로 다뤘던 K-means 군집분석은 시각화해보았을 때 원형 형태의 데이터를 잘 군집화 시킨다고 하고, 두 번째로 다뤘던 혼합분포 군집분석은 타원 형태로 데이터를 잘 군집시킨다는 말을 읽은 적이 있다.
하지만 직접 실습해 보고 정리하면서 그 부분은 잘 느끼지 못했다.
실생활에서 데이터는 원형이나 반달형태보다는 정규분포의 형태를 지닌다고 한다.
그래서 실생활의 데이터분석에서는 혼합분포 군집분석이 더 적합한 경우가 많다는 참고서의 조언이다.
'내가 하는 데이터분석 > 내가 하는 통계분석' 카테고리의 다른 글
| [시계열 분석, Timeseries Analysis] - 시계열 분해, 정상성 with Python (0) | 2023.01.20 |
|---|---|
| [연관분석, Association Analysis] with Python (0) | 2023.01.18 |
| [군집분석, Clustering] - 계층적 군집분석 with Python (0) | 2023.01.14 |
| [교차분석, ChiSquare Test] with Python (0) | 2023.01.12 |
| [다중 회귀분석, Multiple Regression] - 다중공선성 with Python (0) | 2023.01.10 |



