다중 선형 회귀분석 중에서 필수적으로 해결해야 하는 것인 다중공선성에 대해 정리해보고자 한다.
이 전엔 선형 회귀분석에 대해서 정리해 보았다.
선형 회귀분석(Linear Regression)
하나 혹은 그 이상의 원인(독립변수)이 종속변수에 미치는 영향을 추적해서 식으로 표현하는 회귀분석을 복습해 보자. 회귀분석의 검토사항 모형이 데이터를 잘 적합하고 있는가? 회귀모형이
py-moon.tistory.com
다중공선성 : 다중 회귀분석에서 독립변수들 간에 강한 상관관계가 나타나는 문제
단순 선형 회귀분석과 다중 선형 회귀분석의 차이점은 독립변수의 수이다.
단순 선형 회귀분석 -> 독립변수 1개, 종속변수 1개
다중 선형 회귀분석 -> 독립변수 2개 이상, 종속변수 1개
다중 선형 회귀분석에서 다중공선성을 검사하고 진단한 후에 제거하는 과정을 정리하고자 한다.
|
1
2
3
|
import pandas as pd
Cars = pd.read_csv('data/Cars93.csv')
|
cs |
> 다중 회귀분석에 필요한 데이터를 불러온다.
> Cars데이터에는 많은 변수가 있지만, 우리는 종속변수로 Price, 독립변수로 EngineSize, RPM, Weight, Length, MPG.city, MPG.highway를 가지고 분석을 진행하고자 한다.
|
1
2
3
4
5
6
7
|
import numpy as np
import statsmodels.api as sm
import statsmodels.formula.api as smf
Cars.columns = Cars.columns.str.replace('.','')
model = smf.ols(formula ='Price ~ EngineSize + RPM + Weight + Length + MPGcity + MPGhighway', data = Cars)
result = model.fit()
|
cs |
> 5줄에서 변수에 온점이 있는 경우 제거해 주었다.
> 위 코드에 대한 summary를 통해서 회귀모형에 대한 정보를 얻고자 한다.

> summary테이블을 봤을 때 모델 자체는 유의하다는 결과를 보여주지만(Prob F-statistic) 이 모델이 전체 데이터를 설명하는 비율이 54.2%로 나온 것을 보았을 때 현재까지는 직관으론 그리 좋은 모델이라고 보기엔 어렵다는 것이다.
> 다음은 다중 공선성을 진단해 보자.
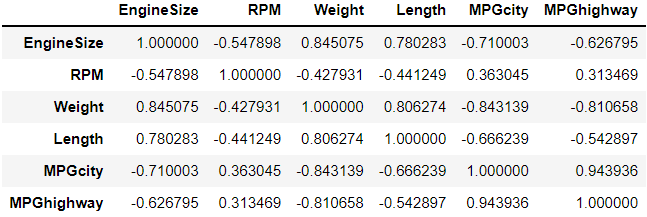
> 독립변수들 간의 상관계수를 확인함으로써 다중 공선성을 진단해본 결과,
> MPGcity변수와 MPGhighway변수가 약 0.94의 높은 양의 상관관계를 보이고 있다.
> 따라서 다중공선성 문제가 있다고 판단하지만, 둘 중 어느 변수를 제거해야 하는지를 모른다.
> 이번엔 VIF(Variance Inflation Factor) 값을 통해서 추려내보고자 한다. 일반적으로 VIF값이 10 이상이면 다중 공선성을 예상한다.
|
1
2
3
4
5
6
7
8
9
|
from patsy import dmatrices
from statsmodels.stats.outliers_influence import variance_inflation_factor
y, X = dmatrices('Price ~ EngineSize + RPM + Weight + Length + MPGcity + MPGhighway', data=Cars, return_type='dataframe')
vif_list=[]
for i in range(1, len(X.columns)):
vif_list.append([variance_inflation_factor(X.values, i), X.columns[i]])
pd.DataFrame(vif_list, columns=['vif', 'variable'])
|
cs |
> VIF값을 알 수 있는 코드를 통해 확인해 보자.

> 결과를 보니 MPGcity변수가 VIF값이 약 13.6으로 MPGhighway변수보다 높으므로 MPGcity변수를 제거해야겠다는 생각이 든다.
> 해당 변수를 제거하고 다시 회귀모델을 살펴보자.

> 변수를 제거한 후 결과를 보니 모델 자체는 여전히 유의하지만 설명력도 여전히 낮다. 변화가 있긴 하지만 눈에 띌 정도는 아니라고 본다.
> 그렇다면, 이번에는 변수 선택법을 통해서 독립변수 중 유의한 변수를 고르고 모델의 성능을 최적화시켜보도록 하자.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
|
import time
import itertools
def processSubset(X, y, feature_set):
model = sm.OLS(y, X[list(feature_set)])
regr = model.fit()
AIC = regr.aic
return {'model':regr, 'AIC':AIC}
# 전진선택법
def forward(X, y, predictors):
remaining_predictors = [p for p in X.columns.difference(['Intercept']) if p not in predictors]
results = []
for p in remaining_predictors:
results.append(processSubset(X=X, y=y, feature_set = predictors + [p] + ['Intercept']))
models = pd.DataFrame(results)
best_model = models.loc[models['AIC'].argmin()]
print('Processed ', models.shape[0], 'models on ', len(predictors)+1, 'predictors in')
print('Selected predictors: ', best_model['model'].model.exog_names, 'AIC:', best_model[0])
return best_model
# 후진소거법
def backward(X, y, predictors):
tic = time.time()
results = []
for combo in itertools.combinations(predictors, len(predictors) -1):
results.append(processSubset(X=X, y=y, feature_set = list(combo) + ['Intercept']))
models = pd.DataFrame(results)
best_model = models.loc[models['AIC'].argmin()]
toc = time.time()
print('Processed ', models.shape[0], 'models on ', len(predictors)-1, 'predictors in', (toc - tic))
print('Selected predictors: ', best_model['model'].model.exog_names, 'AIC:', best_model[0])
return best_model
# 단계적 선택법
def Stepwise_model(X, y):
Stepmodels = pd.DataFrame(columns = ['AIC', 'model'])
tic = time.time()
predictors = []
Smodel_before = processSubset(X, y, predictors + ['Intercept'])['AIC']
for i in range(1, len(X.columns.difference(['Intercept'])) +1):
Forward_result = forward(X=X, y=y, predictors=predictors)
print('Forward')
Stepmodels.loc[i] = Forward_result
predictors = Stepmodels.loc[i]['model'].model.exog_names
predictors = [k for k in predictors if k != 'Intercept']
Backward_result = backward(X=X, y=y, predictors=predictors)
if Backward_result['AIC'] < Forward_result['AIC']:
Stepmodels.loc[i] = Backward_result
predictors = Stepmodels.loc[i]['model'].model.exog_names
Smodel_before = Stepmodels.loc[i]['AIC']
predictors = [k for k in predictors if k != 'Intercept']
print('Backward')
if Stepmodels.loc[i]['AIC'] > Smodel_before:
break
else:
Smodel_before = Stepmodels.loc[i]['AIC']
toc = time.time()
print('Total elapsed time:', (toc - tic), 'seconds.')
return (Stepmodels['model'][len(Stepmodels['model'])])
|
cs |
> 위 코드는 [파이썬 한 권으로 끝내기]를 참고하여 작성한 코드이다.
> 위에서 진행하는 변수 선택법은 AIC값을 기준으로 변수를 선택하거나 제거하는 방식을 사용했다.
> 각 시행마다 AIC값을 계산하여 높은 AIC값을 유발하는 변수는 제거하였다.
> 유의한 변수를 찾거나 방해가 되는 변수를 제거하는 전진선택법, 후진소거법, 단계적선택법을 사용을 하는 것도 좋지만, 그 알고리즘을 이해하는 것도 역량을 성장시킬 수 있는 방법 중 하나라고 생각한다.
> 위 코드를 실행시킨 모델의 summary를 확인해보자.

> 결과적으로 마지막에 남은 변수는 Weight, RPM, EngineSize 세 변수이다.
> 모델이 데이터를 약 54.7%를 설명하고 있지만, 높은 설명력이 아니므로 다른 추가적인 과정을 거쳐야할 것으로 보인다.
> 이 모델이 의미하는 회귀식은 y = 0.0073Weight + 0.0071RPM + 4.3054EngineSize - 51.7933 이다.
OUTTRO.
다중회귀분석을 많이 사용하지만 다중공선성 문제를 필수적으로 해결하려하지 않았던 지난 분석들을 돌아본다.
물론 최근에는 없지만 "필수적"이라는 수식어 때문에 괜히 찔리는 듯 하다.
다중회귀분석을 사용할 때 다중공선성을 상관계수, VIF, 변수선택법 등을 통해서 해결한다면 더 좋은 성능과 설명력을 가질 수 있다.
물론, 다중공선성이 모델 성능의 전부는 아니지만 꼭 해결해야하는 문제임을 상기시킨다.
'내가 하는 데이터분석 > 내가 하는 통계분석' 카테고리의 다른 글
| [군집분석, Clustering] - 계층적 군집분석 with Python (0) | 2023.01.14 |
|---|---|
| [교차분석, ChiSquare Test] with Python (0) | 2023.01.12 |
| [선형 회귀분석, Linear Regression] with Python (0) | 2023.01.08 |
| [이원배치 분산분석, Two-way ANOVA] with Python (0) | 2023.01.06 |
| [일원배치 분산분석, One-way ANOVA] with Python (0) | 2023.01.02 |



