각 범주에 따른 종속변수의 분포를 설명하거나, 두 변수가 서로 연관성이 있는지를 검정하는 교차분석 즉, 카이제곱 검정을 통해 정리해 보자.
이전엔 다중 회귀분석과 다중공선성에 대해서 정리해 보았다.
다중 회귀분석 - 다중공선성
다중 선형 회귀분석 중에서 필수적으로 해결해야 하는 것인 다중공선성에 대해 정리해보고자 한다. 다중공선성 : 다중 회귀분석에서 독립변수들 간에 강한 상관관계가 나타나는 문제 단순 선형
py-moon.tistory.com
이전에 T검정과 분산분석에서는 종속변수가 연속형 변수였지만 카이제곱 검정은 독립변수, 종속변수 둘 다 범주형 변수인 경우에 사용한다.
카이제곱 검정은 검정의 목적에 따라 3가지 검정으로 분류된다.
- 관찰빈도가 기대분포를 따르는지 검정하는 경우 -> 적합성 검정
- 두 개 이상의 변수가 서로 독립인지 검정하는 경우 -> 독립성 검정
- 두 집단의 분포가 서로 동일한지 검정하는 경우 -> 동질성 검정
관찰빈도 : 데이터로부터 얻은 빈도분포
기대빈도 : 두 변수가 독립일 때 이론적으로 기대할 수 있는 빈도분포
적합성 검정
|
1
2
3
|
import pandas as pd
df = pd.read_csv('data/titanic.csv')
|
cs |
> 적합성 검정을 위해 타이타닉 데이터를 활용하고자 불러온다.
|
1
2
3
4
5
6
|
df_t = df[df['survived']==1]
table = df_t[['sex']].value_counts()
female 233
male 109
|
cs |
> 타이타닉 데이터 중 생존자데이터만 추출한 후 성별을 뽑아보았다.
> 여성은 233명, 남성은 109명으로 확인된다.
|
1
2
3
|
from scipy.stats import chisquare
chi = chisquare(table, f_exp=[171, 171])
|
cs |
> 생존자는 총 342명으로 절반은 171명이다.
> 우리는 여기서 적합성 검정을 수행하기 위해 가설을 세운다.
귀무가설 : 타이타닉호의 생존자 중 남자의 비율이 50%, 여자의 비율이 50%이다.
대립가설 : 타이타닉호의 생존자 중 남자의 비율이 50%, 여자의 비율이 50%라고 할 수 없다.
> 위 가설을 검정하기위해 chisqare()를 활용했다.
|
1
|
Power_divergenceResult(statistic=44.95906432748538, pvalue=2.0119672574477235e-11)
|
cs |
> 결과는 유의확률(pvalue)이 유의 수준(0.05) 보다 낮으므로 귀무가설 기각하고 대립가설을 채택한다.
> 즉, 타이타닉호의 생존자 중 남자의 비율이 50%, 여자의 비율이 50%라고 할 수 없다는 결과다.
독립성 검정
|
1
2
|
df = pd.read_csv('data/titanic.csv')
table = pd.crosstab(df['class'], df['survived'])
|
cs |
> 독립성 검정을 위해 타이타닉 데이터 중 객실 등급 변수와 생존여부 변수를 활용한다.
> 이를 crosstab()을 통해 테이블로 추출해 보았다.
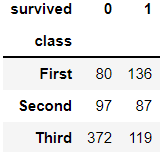
> 테이블을 보면 확인할 수 있듯이 생존여부에 따른 객실 등급을 한눈에 확인할 수 있다.
> 생존자 중에선 1등급 탑승객이 많고, 사망자 중에선 3등급 탑승객이 많다는 인사이트를 도출할 수 있다.
|
1
2
3
|
from scipy.stats import chi2_contingency
chi, p, df, expect = chi2_contingency(table)
|
cs |
> 위 테이블을 활용해서 독립성 검정을 시행해 보자.
귀무가설 : class 변수와 survived 변수는 서로 독립이다.
대립가설 : class 변수와 survived 변수는 서로 독립이 아니다.
|
1
2
3
4
5
6
|
Statistic : 102.88898875696056
p-value : 4.549251711298793e-23
df : 2
expect :[[133.09090909 82.90909091]
[113.37373737 70.62626263]
[302.53535354 188.46464646]]
|
cs |
> 시행 결과는 유의확률(p-value)이 유의 수준(0.05) 보다 낮으므로 귀무가설 기각하고 대립가설을 채택한다.
> 즉, class 변수와 survived 변수는 서로 독립이 아니라는 결과이다.
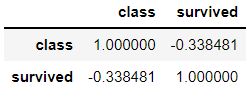
> 도출된 결과에 대해서 상관계수를 확인해 본 결과 음의 상관관계가 있어 보인다.
동질성 검정
> 동질성 검정은 독립성 검정과 같은 검정방법을 가지지만 다른 가설을 가진다.
귀무가설 : class변수의 분포는 survived변수에 관계없이 동일하다.
대립가설 : class변수의 분포는 survived변수에 관계없이 동일하지 않다.
> 검정 결과에 따라 해당 가설을 채택하면 된다.
OUTTRO.
통계분석은 변수의 자료형에 따라 검정하는 방식이 다름을 알고 있어야 한다.
교차분석 즉, 카이제곱검정은 독립변수, 종속변수 둘 다 범주형 자료형 일 때 사용가능한 방법이다.
그 안에서도 목적에 따라 3가지 방식(적합성, 독립성, 동질성)으로 검정할 수 있는 방법이 있기에 이를 활용한다면 유용한 인사이트를 도출할 수 있을 것이다.
'내가 하는 데이터분석 > 내가 하는 통계분석' 카테고리의 다른 글
| [군집분석, Clustering] - 비계층적 군집분석 with Python (4) | 2023.01.16 |
|---|---|
| [군집분석, Clustering] - 계층적 군집분석 with Python (0) | 2023.01.14 |
| [다중 회귀분석, Multiple Regression] - 다중공선성 with Python (0) | 2023.01.10 |
| [선형 회귀분석, Linear Regression] with Python (0) | 2023.01.08 |
| [이원배치 분산분석, Two-way ANOVA] with Python (0) | 2023.01.06 |



